
アマ無線4級問題、インピーダンス計算問題の復習と確認!暗記だけでは解答できない計算問題の復習ポイントです。
オームの法則・単位
「V」はボルトと読み、電圧( E )の単位です。電気を流そうとする力の大きさになります。水道で例えると、水圧つまり流れようとする力ですね。
「Ω」はオーム読み、抵抗( R )の単位です。 電流の流れを妨げようとする力抵抗です。ゴムやガラスなどの不導体は電気抵抗が極端に大きく、電気を通しません。電気を通しやすいものを、導体 と言います。
「A」はアンペアと読み、電流( I )の単位です。 水道で例えると、水量つまり流れている量ですね。
I(A) = E(V)÷ R( Ω )
この式を変形することで、
E(V) = I(A) × R( Ω )
R( Ω ) = E(V) ÷ I(A)
抵抗値の計算、直列接続・ 並列接続の計算 の仕方は・・・。
無線技士資格・工学問題の復習ポイント をご覧ください。
インピーダンスの計算
インピーダンスとは、交流回路における抵抗のようなもので、単位も抵抗と同じくオーム [Ω] を使います。
インピーダンスの計算をしようとする場合には、複素数が入ってきて、記号法で計算するとなるとちょっと分かりづらいですね。ここでは、インピーダンスの計算法について 説明します。
抵抗とコイルの合成インピーダンスを計算してみます。
例題
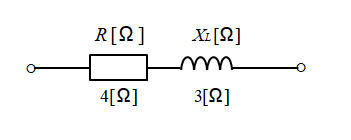
抵抗とコイルの直列接続の、インピーダンス Z は次のようになります。
(注)j とは、虚数を表す記号です。(交流成分に対する抵抗値としてあらわすための記号)
Z = R + jXL
( +jになることに注意)
| Z | = √R2 + X2L ( √** : ルート計算です)
ここで、R = 4 [Ω]、XL = 3 [Ω] とすると
Z = 4 + j3
| Z | = √4の2乗 + 3の2乗 = √16+9 =√25 = 5 [Ω] となります。
抵抗とコンデンサの合成インピーダンスを計算してみます。
例題
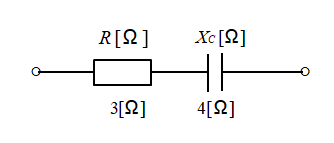
抵抗とコンデンサの直列接続の、インピーダンス Z は次のようになります。
Z = R − jXC
( -jになることに注意)
| Z | = √R2 + X2C ( √** : ルート計算です)
ここで、R = 3 [Ω]、XC = 4 [Ω] とすると
Z = 3 − j4
| Z | = √3の2乗 + 4の2乗 = √16+9 = √25 =5 [Ω] となります。
(注) 3 − j4 なのにどうして 足し算するの? それは、j のつく虚数成分はベクトルの絶対値で扱うからです。
インピーダンスの並列接続の計算は、次のようになります。
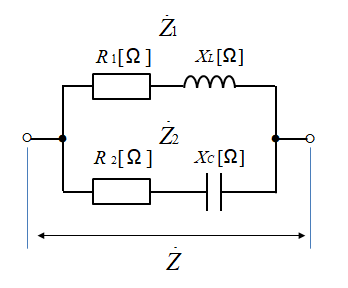
Z = 1÷((1÷Z1) + (1÷ Z2))
Z1 =( R1 + jXL )
Z2 = ( R2 - jXC )
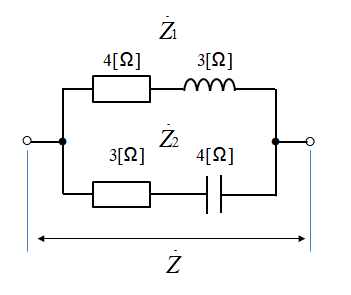
1/Z=(1/4+j3)+(1/3−j4 ) (並列の計算式になります)
Z =1÷ ((1/4+j3)+(1/3−j4 )) ・・・ Z=の計算に変換すると
Z1 = 5(Ω)、 Z2 = 5 (Ω) を当てはめると、
Z = 1÷ ((1/5)+(1/5 ))
= 1÷(2/5)
= 5/2 = 2.5( Ω) となります。
逆数から、Z を求めて計算することができますが、並列回路の場合は、アドミタンスとして逆数のままで計算するほうが良いこともあります。












